麦克斯韦方程组详解|全面解析最美物理公式( 二 )

我们还可以做这样的实验：将一根磁铁插入螺线管，螺线管连接到一个电流表上，也会发现电流表上有读数。这也满足法拉第所说的“在运动和变化的过程中，磁场可以产生电流。”

通过奥斯特、法拉第等人的发现，人们认识到电和磁并不是割裂的，而是紧密相关的，甚至有人认为：电和磁似乎是同一个问题的两个方面。
麦克斯韦方程组的数学基础1860年，比法拉第年轻四十岁的青年科学家麦克斯韦来到了法拉第面前，他把他之前发表的论文《论法拉第的力线》递交给法拉第。法拉第大喜过望，并对麦克斯韦说：你不应该局限于用数学解释我的观点，而要有所创新。

在法拉第的鼓励下，麦克斯韦进一步开拓了自己的观点，并最终总结成四个方程组成的麦克斯韦方程组。为了理解这四个方程，我们首先需要两种数学运算：通量和路径积分。
第一个概念是通量。如果电场E垂直穿过一个平面S，我们把电场E和面积S的乘积称为电场通量。如果电场E和平面S的法线夹一定的夹角，我们可以把电场进行正交分解，再用垂直于平面的分量乘以面积得到电场通量。

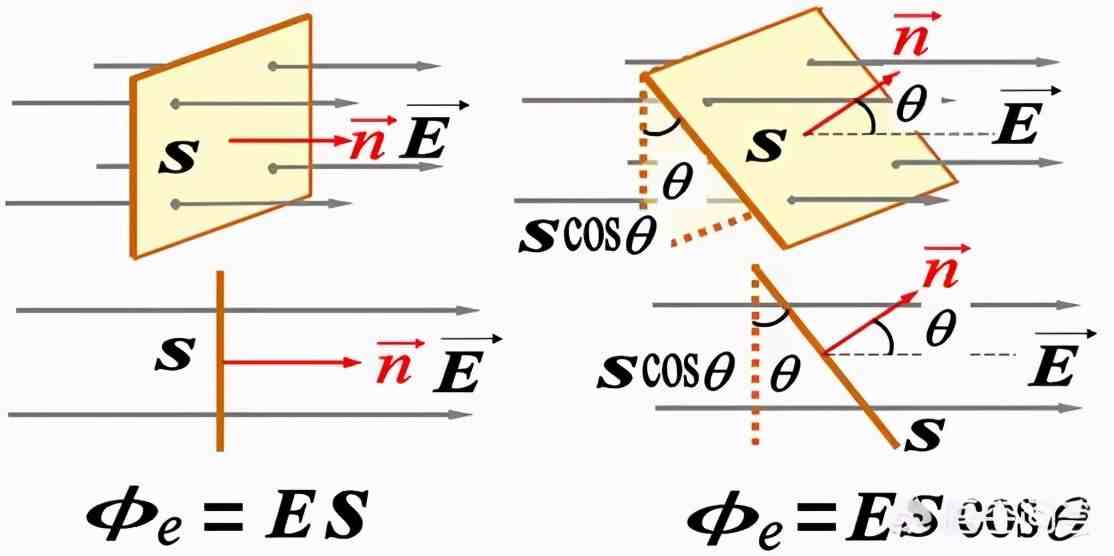
因为电场E可以用电场线的疏密表示，所以用电场E乘上面积S，实际上表示的就是穿过这个面的磁感线根数。假如各处电场不同，就需要把面积分割成无限多份，用每一小份的电场通量相加。

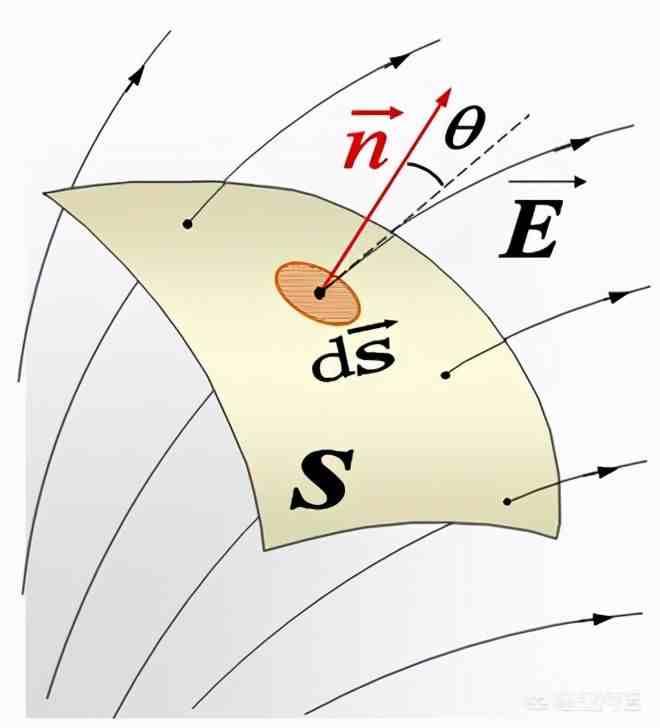
用数学表达式表示就是：

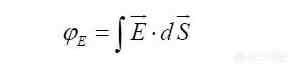
同样，磁场穿过一个面时也可以用同样的方法定义磁通量。用积分符号写作：

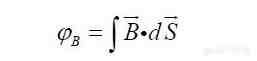
第二个概念是路径积分。如果一个电场E沿着路径AB的方向，用电场E乘以路径AB的长度L，就得到路径积分。如果电场E与路径AB方向夹一定角度，就把电场进行分解，把沿着AB方向的场分量乘以路径长度L 。磁场也有类似的路径积分。

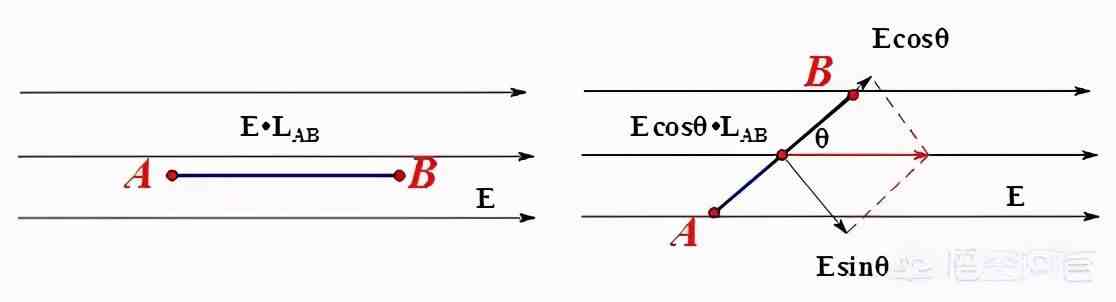
如果电场或磁场各处不同，我们就可以把路径AB分成无穷多份，把每一份的路径积分加起来，表示成：

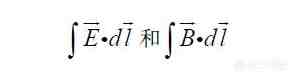
需要注意路径并不一定是直线，沿着曲线也有路径积分。
麦克斯韦方程组好了，现在我们知道了一个矢量可以计算通量，也可以计算路径积分。这样我们就可以来理解这四个伟大的方程了。
1.电场的有源性
麦克斯韦方程组的第一个方程用数学表示了法拉第的第一个观点：电荷会在周围空间产生电场。正电荷会向外发射电场线，负电荷会从周围吸收电场线。电荷的电量越大，所发射或者吸收的电场线越多。
如果我们用一个闭合曲面包围住一个电荷，那么这个闭合曲面上的电场通量就代表了电场线的根数。由于这些电场线都是由曲面内的电荷发射出来的，所以它正比于曲面内所有电荷的代数和。需要注意的是：无论我们所选取的曲面形状如何，只要它包围的电荷相同，它的电通量就是相同的。如果电荷在闭合曲面外，它发射的电场线就既要穿入曲面，又要穿出曲面，这样对曲面的电通量就没有贡献，因此在方程中考虑的电荷量都是曲面内部的电荷。

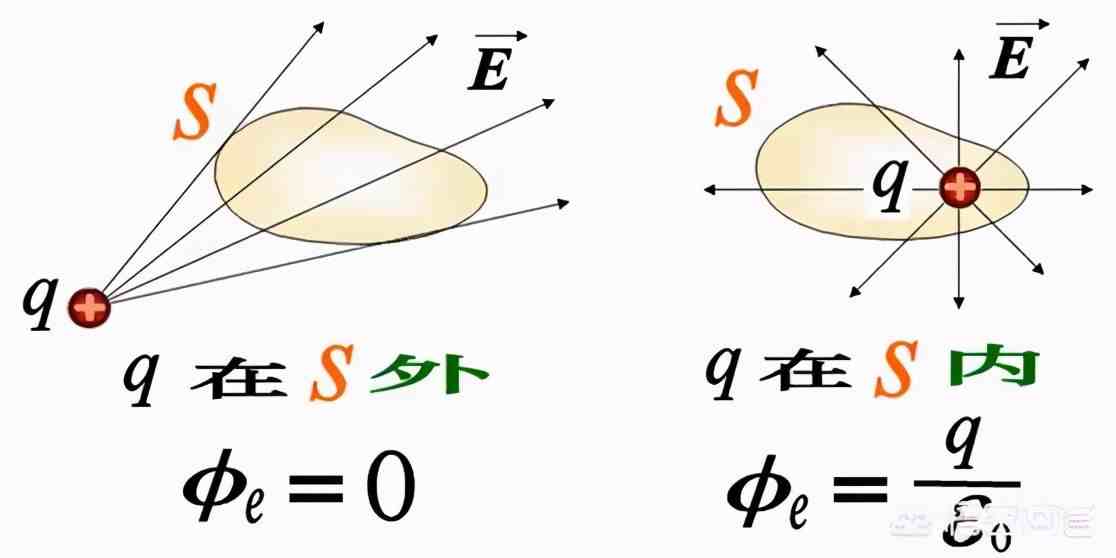
用公式写作

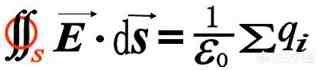
在这个公式中，等号左边部分表示闭合曲面上的电通量，也就是穿出曲面的电场线根数，等号右边的q表示曲面内的电荷代数和，0称为真空介电常数。这个方程就是麦克斯韦方程组中的第一个方程，也称为电场高斯定律。这个方程告诉我们：电场是有源场，它的源就是空间中的电荷。
2. 磁场的无源性
与电场不同，无论是由磁体产生的磁场，还是由电流产生的磁场，磁感线总是闭合的。磁感线既没有出发点，也没有结束点。比如我们观察通电螺线管的磁场就会发现这个特点。

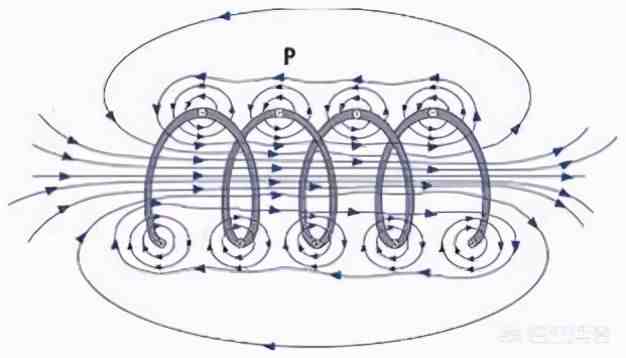
于是，如果我们在空间中做一个闭合曲面，磁感线要么不穿透这个曲面，要么一定是既穿入这个曲面，又穿出这个曲面，因此磁感线的通量为零。