微分中值定理|如何理解三大微分中值定理？( 二 )

设函数满足以下两个条件：
在闭区间 [a,b] 上连续
在开百思特网区间 (a,b) 上可导
则存在

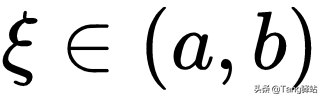
这个定理的几何意义就是，至少存在一点的切线与端点的连线平行；物理意义是，百思特网至少存在一点的速度与平均速度相等：

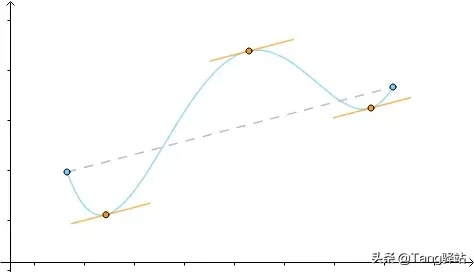
把它旋转一下，
得到的就是罗尔中值定理，可见罗尔是拉格朗日的特例：

3 柯西中值定理
设函数
满足以下条件：
在闭区间 [a,b] 上连续
在开区间 (a,b) 上可导
有：
则存在

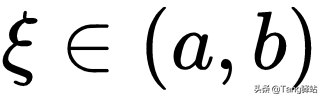
，使等式

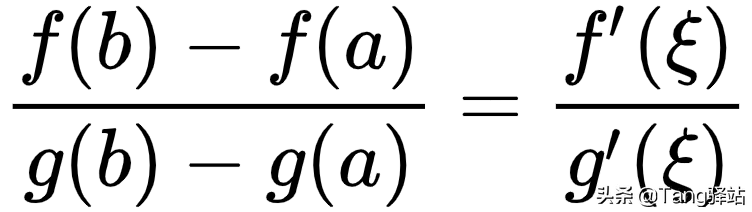
成立。
可以把

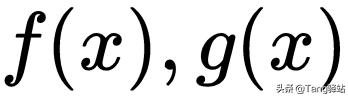
组合成参数方程：

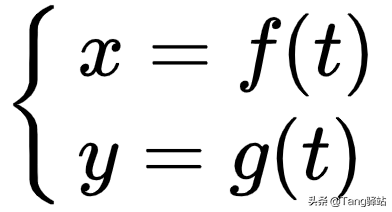
这样柯西中值定理就有类似于拉格朗日中值定理一样的几何意义：

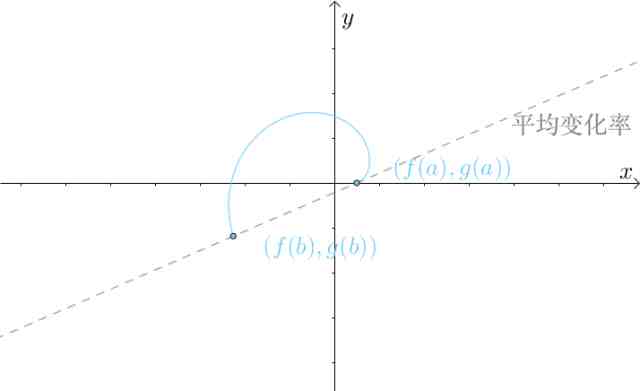
如果：

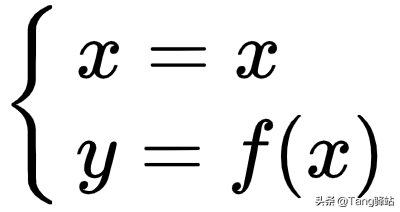
那么柯西中值定理就变为了拉格朗日中值定理，所以拉格朗日又是柯西的特例。

4 总结
三大微分中值定理的联系与区别：

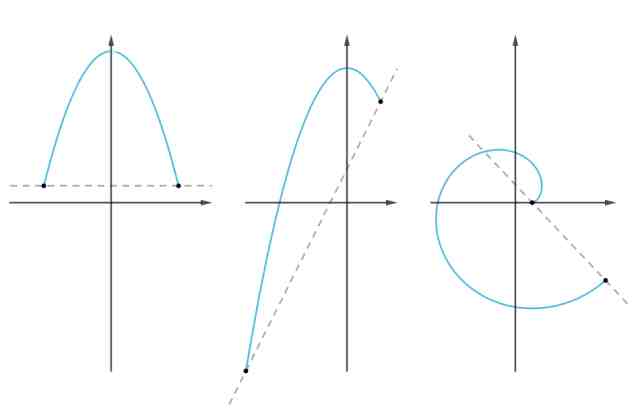
微分中值定理是微分学中最重要的基本定理之一，是沟通函数与其导数之间的桥梁，是应用导数的局部性质研究函数在区间上的整体性质的重要工具，也是不等式与等式证明的重要方法。因此，关于微分中值定理的学习与研究具有非常重要的实际应用与理论意义。