科学家小时候的故事|爱因斯坦的童年( 五 )

学过几何的读者都知道，几何的证明——乃至其他数学证明——是要从公理、定义等等出发的，从而离不开某种体系。爱因斯坦既然尚未学过“神圣的几何学小书”，他是怎百思特网样证明毕达哥拉斯定理的呢？这个有趣的问题虽无第一手的答案，但依据爱因斯坦留下的片言只语的线索，人们已能很有把握地复现他的证明。在晚年自述中，爱因斯坦提供了一条线索：即他的证明用到了直角三角形的“相似性”（考虑到他当时尚未学过几何，这一术语当是回忆时的借用）。具体地说，他认为足够显然——从而可作为证明依据的是：“直角三角形各边的关系完全取决于它的一个锐角”（换句话说，两个直角三角形若有一个锐角相同，则彼此“相似”）。另一条线索则出现在波兰哲学家亚历山大莫兹科夫斯基 (Alexander Moszkowski) 1921年出版的Einstein The Searcher : His Work Explained From Dialogues With Einstein（《探索者爱因斯坦：通过与爱因斯坦的对话解读他的工作》）一书中。莫兹科夫斯基是爱因斯坦的朋友，他这本书记录了与爱因斯坦的很多对话及来自对话的信息，其中提到爱因斯坦在证明中作了一条从直角三角形的直角顶点到对边的垂线。

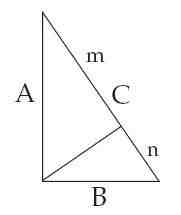
依据这两条线索便可以很有把握地复现爱因斯坦的证明。上图画出了一个直角三角形及从直角顶点到对边的垂线，并对各线段作了标注：A、B、C是直角三角形三条边的长度，m、n为斜边被垂线分成的两个线段的长度。显然，图中的两个小直角三角形分别跟大直角三角形共享一个锐角，从而“各边的关系”完全相同。因此：A/C=m/A，B/C=n/B；略微变形后可得：A^2=mC，B^2=nC，因此A^2+B^2=(m+n)C=C^2 。证毕。这个证明用到了爱因斯坦给出的两条线索，且只用到了那两条线索，故极有可能就是爱因斯坦的证明。虽尚未读过“神圣的几何学小书”，证明毕达哥拉斯定理的这一努力还是让童年爱因斯坦领会到了数学证明的一个重要特点，那就是“只有……不‘显然’的东西才需要证明” 。有了这种领会，当他读到“神圣的几何学小书”时，对公理的存在及必须不加证明地接受公理这一特点就并不觉得困扰了。
1894年，因生意经营不善，爱因斯坦一家从慕尼黑迁往意大利，只留了爱因斯坦在慕尼黑读中学。按部就班的话，爱因斯坦尚需三年时间才能读完中学，但该年年底（12月29日），爱因斯坦就从家庭医生——恰好是塔耳玫的哥哥——处弄到了一纸医生证明，以“健康原因”退了学[注9] 。爱因斯坦并且还得到了路特波德中学一位老师的“推荐信”，对他的数学知识和数学能力给予了赞许。就这样，爱因斯坦“辍学”离开了路特波德中学，赴意大利与家人团聚 (这么大的事自作主张，幸亏他父母不是什么“虎妈”、“狼爸”，否则焉有宁日) 。不久之后，爱因斯坦申请放弃德国国籍，并于1896年1月28日获得了批准[注10] 。
关于爱因斯坦的童年，大致就写到这里。本文——及拟在未来一段时间撰写的有关爱因斯坦的若干其他文章——是随笔，也可以算读书笔记，可归入我“自创”的所谓“理科书话”之中。既是随笔，自然不会——也不必——面面俱到。事实上，有关爱因斯坦的文献汗牛充栋，面面俱到别说办不到，哪怕能办到，也势必包含太多已被别人重复过太多遍的东西，不如只拣一些我想写的方面来写，其中起码会有一些——且希望所占的比例并不小——是不太容易从普通读物里读到的。这是本文——以及我的所有随笔类文字——在内容取舍上的基本原则。
作为本文的尾声，我们来欣赏一幅爱因斯坦在路特波德中学的集体照——摄于1890年。爱因斯坦站在第一排右数第三，是相片上唯一面带微笑的小孩。

注释
1. “十一时半”常被转述成“11时30分”或“11:30”，不过对于熟悉精度概念的人来说，这种转述是有些别扭的。因为当一个“物理量”的数值不带误差时，精度往往由最后一个数字来体现，因此“11时30分”或“11:30”意味着精度是“分”，误差只能在“分”的量级，而“十一时半”是以“半小时”为单位，误差可以大得多——比方说完全可以是“11:18”或“11:43”等等。
2. 确切地说，字面上所载的是“以色列宗教”(israelitischer Religion)，那是犹太教的前身。不过，爱因斯坦的父母其实并不信犹太教——也不信别的宗教。爱因斯坦在晚年自述里曾表示：“我是完全不信宗教的(犹太人)父母的儿子” 。爱因斯坦小时候所受的宗教影响是来自他的远房亲戚及学校。