cnn是什么意思|CNN通俗解析( 二 )

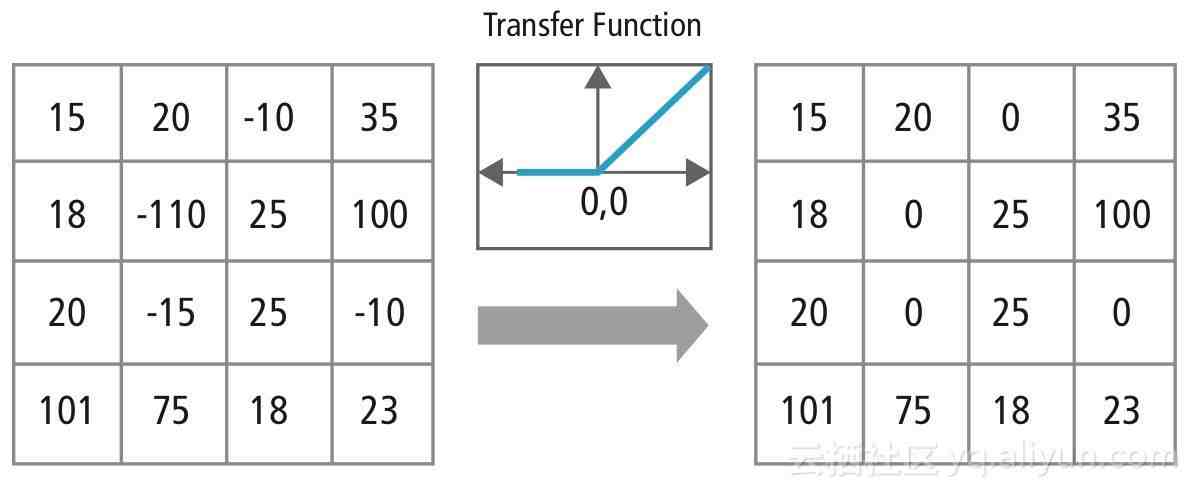
ReLU激活函数
全连接层}Fully Connected Layer：在全连接层中，我们将最后一个卷积层的输出展平，并将当前层的每个节点与下一层的另一个节点连接起来。全连接层只是人工神经网络的另一种说法，如下图所示。全连接层中的操作与一般的人工神经网络中的操作完全相同：

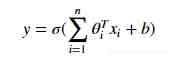
卷积层展开

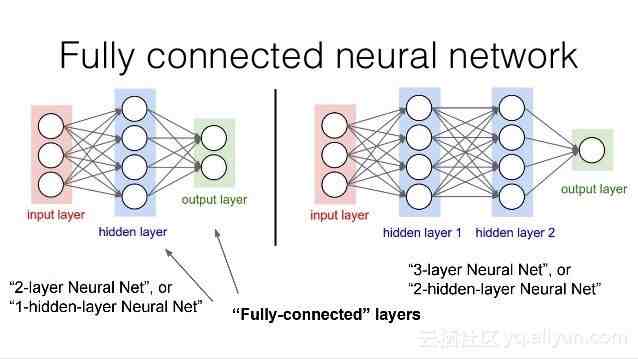
全连接层
上面讨论的层和操作都是每个卷积神经网络的核心组件，现在已经讨论了卷积神经网络在前向传播中经历的操作，下面让我们跳转到卷积神经网络在反向传播中经历的操作。
反向传播|Backpropagation：全连接层：在全连接层中，反向传播与任何常规人工神经网络完全相同，在反向传播中（使用梯度下降作为优化算法），使用损失函数的偏导数即损失函数关于权重的导数来更新参数，其中我们将损失函数的导数与激活输出相乘，激活输出的导数与非激活输出相乘，导数为未激活的输出与权重相对应。
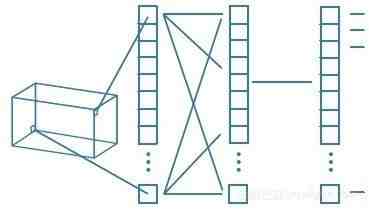
数学表达式如下：

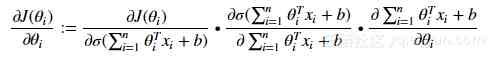
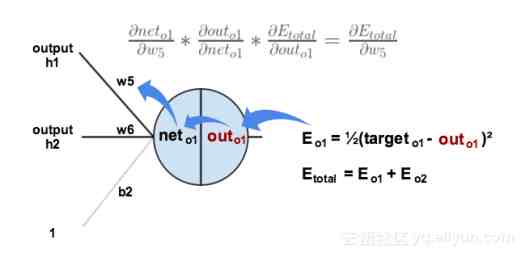
反向传播说明图
在计算梯度之后，我们从初始权重中减去它以得到新的优化：

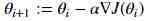
其中：
i+ 1 ：优化的权重
i：初始权重
：学习率
?J（i）：损失函数的梯度

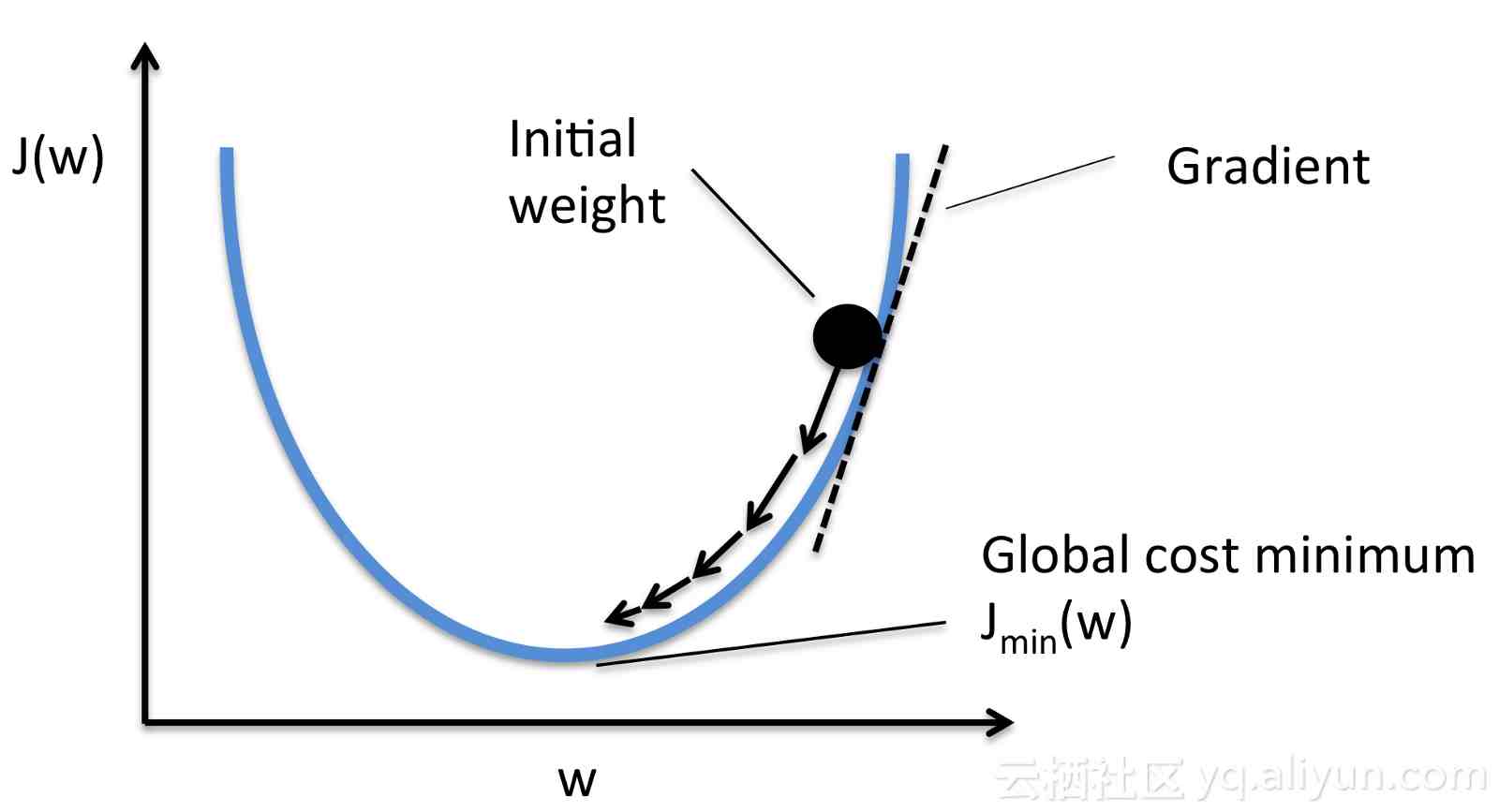
梯度下降
在下面的动态图中，是将梯度下降应用于线性回归的结果。从图中可以清楚地看到代价函数越小，线性模型越适合数据。

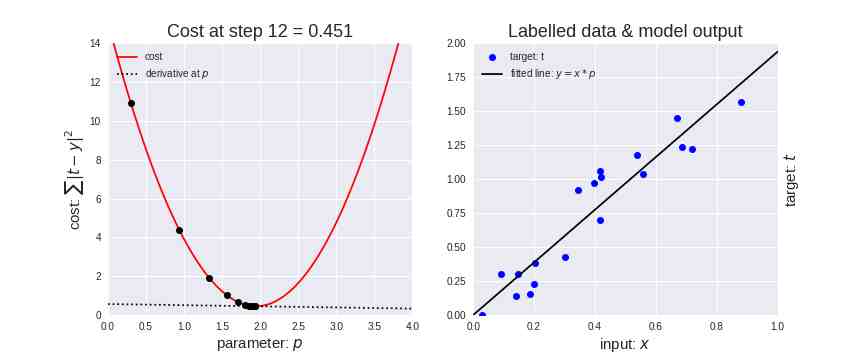
梯度下降应用于线性回归
此外，请注意一点，应该谨慎地选择学习率的取值，学习率太高可能会导致梯度超过目标最小值，学习率太低可能导致网络模型收敛速度变慢。

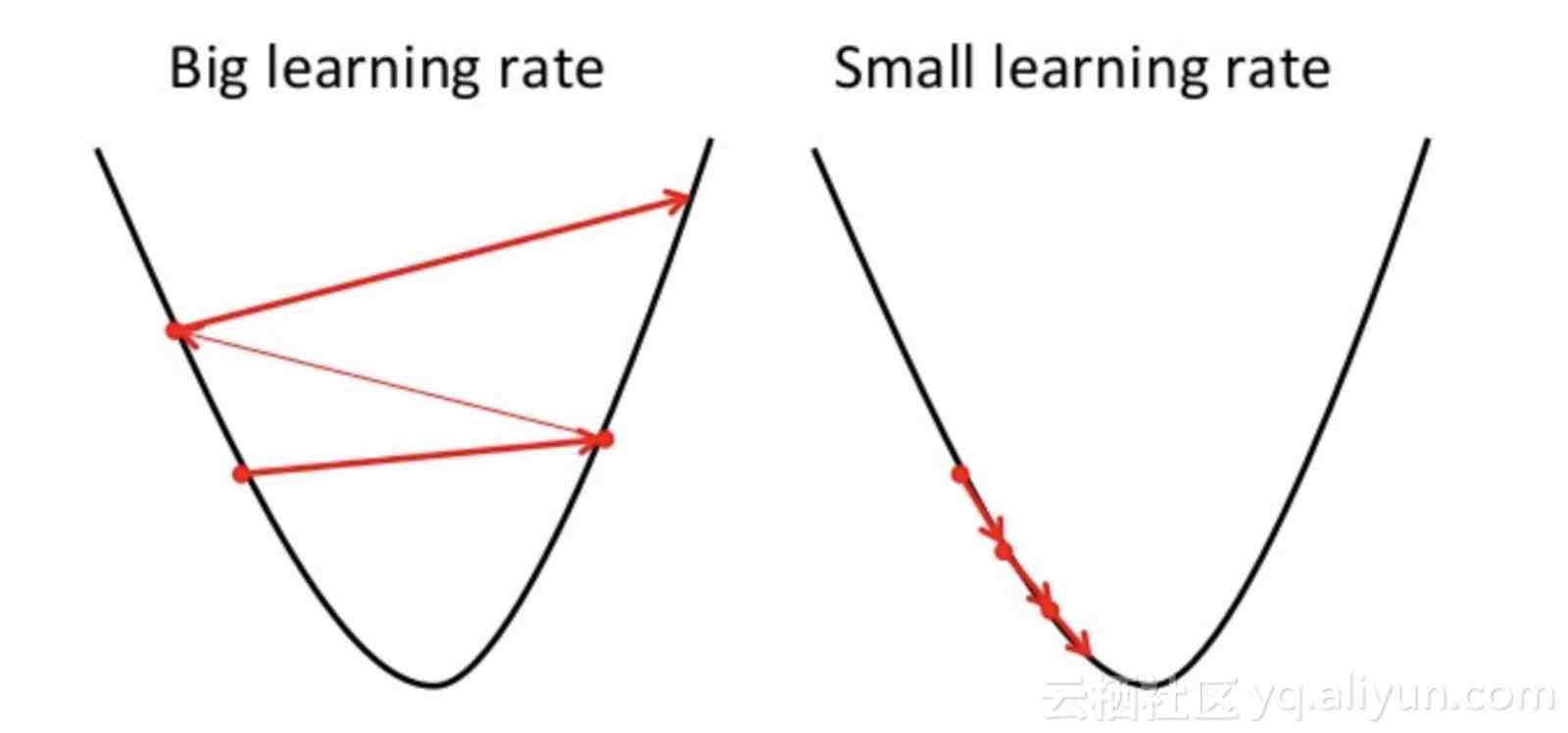
小学习率与大学习率
在所有优化任务中，无论是在物理学、经济学还是计算机科学中，偏导数都被大量使用。偏导数主要用于计算因变量f(x, y, z)相对于其独立变量之一的变化率。例如，假设你拥有一个公司的股份，后者的股票会根据多种因素（证券、政治、销售收入等）上涨或下跌，在这种情况下通过偏导数，你会计算多少股票受到影响而其他因素保持不变，股票发生变化，则公司的价格也会发生变化。
池化层|Pooling Layer：在最大池化特征图层中，梯度仅通过最大值反向传播，因此稍微更改它们并不会影响输出。在此过程中，我们将最大池化操作之前的最大值替换为1，并将所有非最大值设置为零，然后使用链式法则将渐变量乘以先前量以得到新的参数值。

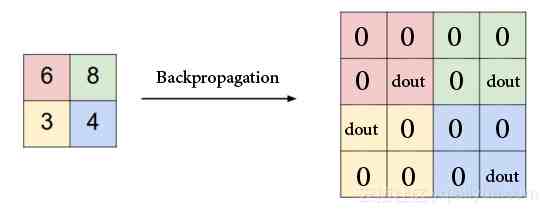
池化层反向传播
与最大池化层不同，在平均池化层中，梯度是通过所有的输入（在平均合并之前）进行传播。
卷积层|Convolution Layer：你可能现在问自己，如果卷积层的前向传播是卷积，那么它的反向传播是什么？幸运的是，它的向后传播也是一个卷积，所以你不必担心学习新的难以掌握的数学运算。

卷积层反向传播
其中：
?hij：损失函数的导数

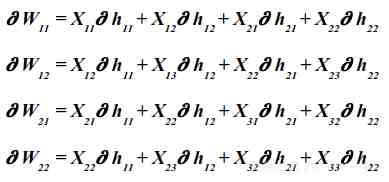
简而言之，上图表明了反向传播是如何在卷积层中起作用的。现在假设你已经对卷积神经网络有了深刻的理论理解，下面让我们用TensorFlow构建的第一个卷积神经网络吧。
TensorFlow实现卷积神经网络：什么是Tensorflow？

TensorFlow是一个使用数据流图进行数值计算的开源软件库。它最初由谷歌机器智能研究机构谷歌大脑团队开发，用于机器学习和深度神经网络的研究。
什么是张量？张量是一个有组织的多维数组，张量的顺序是表示它所需数组的维数。

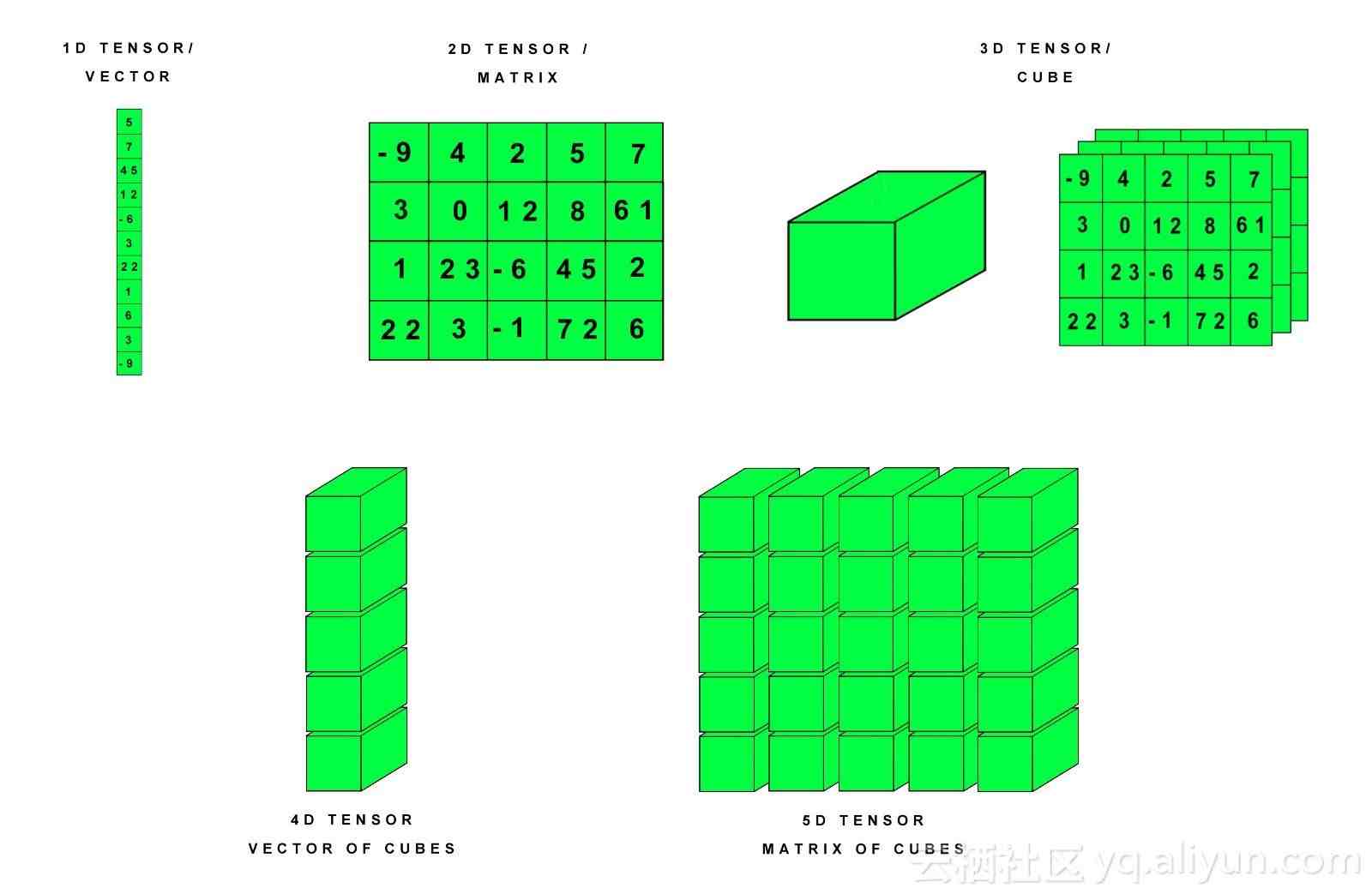
张量的类型
什么是计算图？计算图是计算代数中的一个基础处理方法，在机器学习中的神经网络和其他模型推导算法和软件包方面非常富有成效。计算图中的基本思想是表达一些模型——例如前馈神经网络，计算图作为表示计算步骤序列的一个有向图。序列中的每个步骤对应于计算图中的顶点，每个步骤对应一个简单的操作，每个操作接受一些输入并根据其输入产生一些输出。